Chapitre 3 - Les nombres complexes

Effectuer des calculs algébriques avec des nombres complexes
Résoudre dans $\mathbb{C}$ une équation du second degré
Représentation graphique par un point ou un vecteur

Les nombres complexes apparaîssent en ajoutant à nos nombres classiques un nouveau nombre imaginaire $i$ tel que $i^2=-1$ ! Ca peut sembler idiot et un peu artificiel, de plus on brise un tabou : désormais "un carré ne sera pas toujours positif" !!

En creusant un peu plus, on s'apperçoit qu'avec ces nombres complexes, les polynômes qui n'avaient pas toujours de solution, en on maintenant dans chaque cas (même lorsque $\Delta$ est négatif). Là encore, ça peut sembler un peu étrange de trouver des solutions qui n'existent pas réellement, mais ça a au moins le mérite de simplifier tous ces cas : une solution, deux solutions, pas de solution...

En s'installant dans le paysage mathématique et en le compliquant un peu, les nombres complexes ont en fait permis de simplifier bien des cas, d'apporter des méthodes de résolutions d'équation (avec des solutions bien réelles !!), de construire un pont entre algèbre, analyse et géométrie. Et il s'avèrera même que ces nombres qui n'existent pas dans le monde concret y apparaissent pourtant tout de même comme bien réels dans la physique et l'étude des oscillateurs électriques.

IDéfinition et écriture des nombres complexes

1Introduction

On définit l'ensemble des nombres complexes $\mathbb{C}$ de la manière suivante :

$\mathbb{C}$ contient tous les nombres réels de $\mathbb{R}$
$\mathbb{C}$ contient un nombre $i$ tel que $i^2=-1$
$\mathbb{C}$ contient tous les nombres imaginaires purs, c'est à dire les multiples de $i$ ($2i, \frac{i}{3}, ...$) : $$ b \times i \text{ où } b \in \mathbb{R} $$
$\mathbb{C}$ contient la somme tous nombres complexes (réel et imaginaires purs compris) : $$ a + b i \in \mathbb{C} \text{ pour tous } a,b \text{ réels} $$

Les nombres suivants sont des nombres complexes, et en particulier :

$-1,0,3,\pi, \sqrt{2}, \frac{1}{3}$ ou $0,25$ sont des nombres réels
$i, 2i, \frac{2i\pi}{3}$ sont des nombres imaginaires purs
1+i, 3+2i, \frac{2+3i}{5} sont des nombres complexes.

Pour tout nombre complexe $z \in \mathbb{C}$ s'écrivant $z=a+ib$ ($a,b$ réels), on appelle :

$a$ la partie réelle de $z$. On note $a = Re (z)$
$b$ la partie imaginaire de $z$. On note $a = Im (z)$

On appelle l' écriture $a+ib$ la forme algébrique de $z$.

Soient $z_1=2+i$, $z_2 = 3$, $z_3=\frac{3 + 5i}{2}$. Les parties réelles et imaginaires de ces nombres sont :

$Re (z_1) = 2$ et $Im (z_1) = 1$
$Re (z_2) = 3$ et $Im (z_2) = 0$
$Re (z_3) = \frac{3}{2}$ et $Im (z_2) = \frac{5}{2}$

Si $z$ est un nombre réel, sa partie imaginaire est nulle $Im (z) = 0$.
Si $z$ est un nombre imaginaire pur ($z=b i $, $b$ réel), sa partie réelle est nulle $Re (z) = 0$.

Deux nombres complexes sont égaux si ils ont la même partie réelle et la même partie imaginaire.

2Conjugué d'un nombre complexe

A tout nombre complexe $z=a+ib$ correspond un nombre conjugué noté $\bar{z} = a - i b$ :

Le conjugué de $1+i$ est $1-i$
Le conjugué de $i$ est $-i$
Le conjugué de $2$ est $2$

Soit $z$ un nombre complexe :

$z + \bar{z} = 2 Re (z) $
$z - \bar{z} = 2 i Im (z) $
$z \bar{z} = Re (z)^2 + Im (z)^2 $
$\bar{\bar{z}} = z $

Cliquer pour voir la démonstration

Replier

On commence par poser $z=a + i b$ ($a$ et $b$ réels) :

$z + \bar{z} = a + i b + a - i b = 2 a $
$z - \bar{z} = a + i b - (a - i b) = a + i b - a + i b = 2 b $
$z \bar{z} = (a + i b) (a - i b) = a^2 - (ib)^2 = a^2 - i^2 \times b^2 = a^2 + b^2$
$\bar{\bar{z}} = \overline{\overline{a + i b}} = \overline{a - i b} = a + i b$

La troisième propriété est une nouvelle identité remarquable.

Un exercice courant consiste à mettre sous forme algébrique un quotient de nombre complexe. On utilise alors le conjugué du dénominateur. Par exemple : $$ z = \frac{3+2i}{1-i} $$

Cliquer pour dévoiler la méthode

Replier

$$ \begin{array}{ccll} z &=& \frac{3+2i}{1-i} & \\ &=& \frac{(3+2i)(1+i)}{(1-i)(1+i) } & \text{on fait apparaître le conjugué du dénominateur} \\ &=& \frac{3\times 1 + 3 i + 2 i \times 1 + 2 i \times i (1+i)}{1^2+1^2} & \text{d'après l'identité remarquable } z\bar{z}\\ &=& \frac{3 + 3i + 2i - 2}{2} & \text{maintenant le dénominateur est un nombre réel} \\ &=& \frac{1 + 5i}{2} & \\ &=& \frac{1}{2} + \frac{5}{2} i & \\ \end{array} $$ On a donc $Re (z) = \frac{1}{2}$ et $Im (z) = \frac{5}{2}$

IIPolynômes du second degré

Avec l'apport des nombres complexes, nous avons déjà remarqué que la fonction polynôme définie par $f (x) = x^2 + 1$ possède deux racines imaginaires : $i$ et $-i$. Ca peut être assez déroutant puisque nous savions déjà que ce polynôme a un discriminant négatif et donc aucune racine.... dans $\mathbb{R}$ !

Avec le théorème suivant, nous réalisons qu'en fait n'importe quel polynôme du second degré a des racines dans $\mathbb{C}$ :

Soient $a,b,c \in \mathbb{R}$. On considère l'équation $a z^2 + bz + c = 0$ d'inconnue $z \in \mathbb{C}$.

Cette équation a toujours des solutions complexes (ou réelles). On note $\Delta = b^2 - 4 a c$ le discrimant :

Si $\Delta \gt 0$, l'équation a deux solution réelles $x_1=\frac{-b-\sqrt{\Delta}}{2a}$ et $x_2=\frac{-b+\sqrt{\Delta}}{2a}$
Si $\Delta = 0$, l'équation a une solution réelle $x_0=\frac{-b}{2a}$
Si $\Delta \lt 0$, l'équation a deux solution complexes conjuguées $z_1=\frac{-b-i\sqrt{|\Delta|}}{2a}$ et $x_2=\frac{-b+i\sqrt{|\Delta|} }{2a}$ (avec $z_1=\bar{z_2}$)

En conséquence, le polynôme précédent est toujours factorisable :

Si $\Delta \gt 0$, $az^2+bz+c = a (z-x_1)(z-x_2)$
Si $\Delta = 0$, $az^2+bz+c = a (z-x_0)^2$
Si $\Delta \lt 0$, $az^2+bz+c = a (z-z_1)(z-z_2)$

IIIReprésentation géométrique

1Affixe d'un point

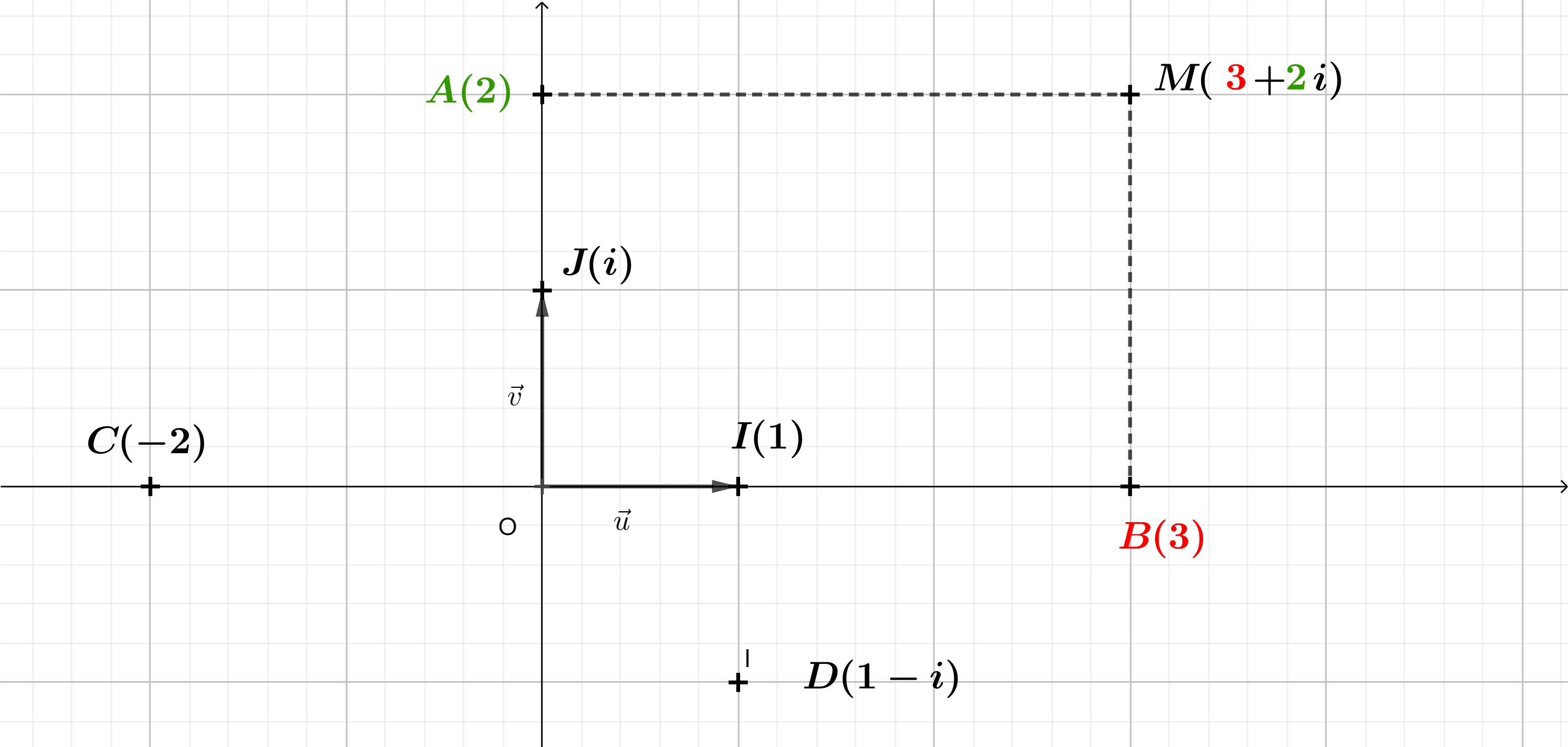
Nous avons déjà l'habitude de représenter géométriquement l'ensemble des nombres réels $\mathbb{R}$ à l'aide d'une droite (la droite réelle) graduées :

Nous pouvons de la même manière représenter géométriquement l'ensemble des nombres imaginaires purs $i \mathbb{R}$ à l'aide d'une droite graduée :

Nous savons que ces deux droites ne possèdent aucune valeur commune sauf 0. Il est donc naturel de les représenter à l'aide d'un repère $(O;\vec{u};\vec{v})$ où les abscisses représentent les réels, les ordonnées les imaginaires purs, et le reste du plan les nombres complexes en général.

Dans cette partie, on se place dans un repère orthonormé $(O;\vec{u};\vec{v})$.

A tout point $M$ du plan de coordonnées $(a;b)$ (noté $M (a;b)$), on peut associer un nombre complexe $z=a+ib$. On dira que le point $M$ a pour affixe $z$ (noté $M (z)$)

Soit $M$ un point d'affixe $z \in \mathbb{C}$ :

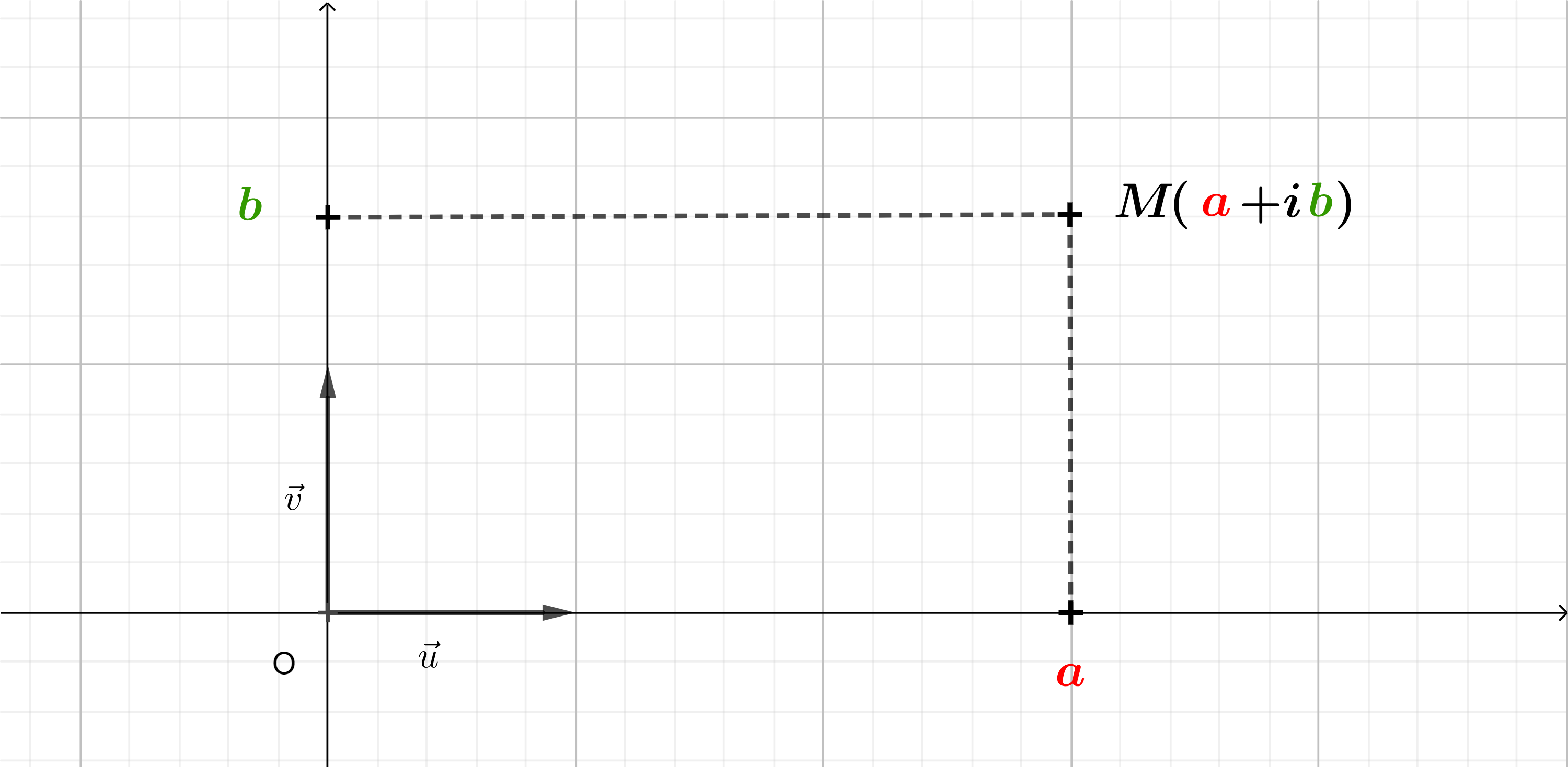
Si $z \in \mathbb{R}$ (réel), alors $M$ appartient à l'axe des abscisses
Si $z \in \mathbb{iR}$ (imaginaire pur), alors $M$ appartient à l'axe des ordonnées

On retrouve la formule du milieu simplifiée par les nombres complexes :

Soient $A (z_A)$ et $B (z_B)$ deux point du plan avec leurs affixes. Soit $M$ le milieu du segment $[AB]$ d'affixe $z_M$. Alors : $$ z_M = \frac{z_A+z_B}{2} $$

Démonstration

Cliquer pour replier

2Affixe d'un vecteur

A tout point $\vec{w}$ du plan de coordonnées $(a;b)$ (noté $\vec{w} (a;b)$), on peut associer un nombre complexe $z=a+ib$. On dira que le vecteur$vec{w}$ a pour affixe $z$ (noté $\vec{w} (z)$)

On retrouve également les formules de calcul de coordonnées de vecteurs, simplifiées par les nombres complexes :

Soient $A (z_A)$ et $B (z_B)$ deux point du plan avec leurs affixes. Le vecteur $\vec{AB} (z)$ a pour affixe $z_B-z_A$

Démonstration

Cliquer pour replier

Soient $\vec{w} (z)$ et $\vec{w'}(z')$ deux vecteurs. On détermine les affixes suivantes :

$\vec{w} + \vec{w'}$ a pour affixex $z+z'$
$-\vec{w}$ a pour affixe $-z$
$k\vec{w}$ a pour affixe $kz$ avec $k \in \mathbb{R}$

3Interprétation géométrique des opérations sur les affixes

Dans la représentation des nombres complexe par le plan, les opération numériques peuvent être interprétées commes des transformations symétriques :

Soit $M (z)$ un point du plan. Alors :

Le point $M'$ d'affixe $-z$ est le symétrique de $M$ par rapport à l'origine.
Le point $M''$ d'affixe $\bar{z}$ est le symétrique de $M$ par rapport à l'axe des ordonnées.
Le point $M'''$ d'affixe $-\bar{z}$ est le symétrique de $M$ par rapport à l'axe des abscisses.